Copyright (C) 2022 Jørgen Schartum Dokken
This file is part of Oasisx SPDX-License-Identifier: MIT
Application of Dirichlet BCs#
Illustrates how to apply bcs to the component of the tentative velocity equation. We compare two strategies:
Using matrix-vector products of pre-assembled matrices to compute the RHS
Assemble the matrix and vector separately We start by importing the necessary modules
# This is a test to check notebooks
import time
import typing
from mpi4py import MPI
from petsc4py import PETSc
import dolfinx
import dolfinx.fem.petsc
import matplotlib.pyplot as plt
import numpy as np
import pandas
import seaborn
import ufl
def assembly(mesh, P: int, repeats: int, jit_options: typing.Optional[dict] = None):
V = dolfinx.fem.functionspace(mesh, ("Lagrange", int(P)))
def f(x):
return 2 * np.sin(x[0]) + 3 + 2 * x[1]
mesh.topology.create_connectivity(mesh.topology.dim - 1, mesh.topology.dim)
boundary_facets = dolfinx.mesh.exterior_facet_indices(mesh.topology)
boundary_dofs = dolfinx.fem.locate_dofs_topological(V, mesh.topology.dim - 1, boundary_facets)
g = dolfinx.fem.Function(V)
g.interpolate(f)
bcs = [dolfinx.fem.dirichletbc(g, boundary_dofs)]
dt = 0.5
nu = 0.3
u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
# Solution from previous time step
u_1 = dolfinx.fem.Function(V)
u_1.interpolate(lambda x: np.sin(x[0]) * np.cos(x[1]))
# Define variational forms
mass = ufl.inner(u, v) * ufl.dx
stiffness = ufl.inner(ufl.grad(u), ufl.grad(v)) * ufl.dx
u_ab = [dolfinx.fem.Function(V, name=f"u_ab{i}") for i in range(mesh.geometry.dim)]
convection = ufl.inner(ufl.dot(ufl.as_vector(u_ab), ufl.nabla_grad(u)), v) * ufl.dx
for u_abi in u_ab:
u_abi.interpolate(lambda x: x[0])
# Compile forms for matrix vector products
jit_options = {} if jit_options is None else jit_options
mass_form = dolfinx.fem.form(mass, jit_options=jit_options)
stiffness_form = dolfinx.fem.form(stiffness, jit_options=jit_options)
convection_form = dolfinx.fem.form(convection, jit_options=jit_options)
# Compile form for vector assembly (action)
dt_inv = dolfinx.fem.Constant(mesh, 1.0 / dt)
dt_inv.name = "dt_inv"
nu_c = dolfinx.fem.Constant(mesh, nu)
nu_c.name = "nu"
rhs = dt_inv * mass - 0.5 * nu_c * stiffness - 0.5 * convection
rhs_form = dolfinx.fem.form(ufl.action(rhs, u_1), jit_options=jit_options)
# Assemble time independent matrices
# Mass matrix
M = dolfinx.fem.petsc.create_matrix(mass_form)
M.setOption(PETSc.Mat.Option.SYMMETRIC, True)
M.setOption(PETSc.Mat.Option.SYMMETRY_ETERNAL, True)
M.setOption(PETSc.Mat.Option.IGNORE_ZERO_ENTRIES, True)
dolfinx.fem.petsc.assemble_matrix(M, mass_form)
M.assemble()
M.setOption(PETSc.Mat.Option.NEW_NONZERO_LOCATIONS, False)
# Stiffness matrix
K = dolfinx.fem.petsc.create_matrix(stiffness_form)
K.setOption(PETSc.Mat.Option.SYMMETRIC, True)
K.setOption(PETSc.Mat.Option.SYMMETRY_ETERNAL, True)
K.setOption(PETSc.Mat.Option.IGNORE_ZERO_ENTRIES, True)
dolfinx.fem.petsc.assemble_matrix(K, stiffness_form)
K.assemble()
K.setOption(PETSc.Mat.Option.NEW_NONZERO_LOCATIONS, False)
# RHS vectors
b = dolfinx.fem.Function(V)
bx = dolfinx.fem.Function(V)
# Timing vectors
oasis_lhs = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
oasis_rhs = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
new_lhs = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
new_rhs = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
new_total = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
oasis_total = np.zeros((repeats, mesh.comm.size), dtype=np.float64)
A_sp = dolfinx.fem.create_sparsity_pattern(mass_form)
A_sp.finalize()
A = dolfinx.cpp.la.petsc.create_matrix(mesh.comm, A_sp)
Ax = dolfinx.cpp.la.petsc.create_matrix(mesh.comm, A_sp)
D = dolfinx.cpp.la.petsc.create_matrix(mesh.comm, A_sp)
D.assemble()
for i in range(repeats):
mesh.comm.Barrier()
# --------------Oasis approach-------------------------
# Zero out time-dependent matrix
start_mat = time.perf_counter()
A.zeroEntries()
A.setOption(PETSc.Mat.Option.KEEP_NONZERO_PATTERN, True)
A.setOption(PETSc.Mat.Option.IGNORE_ZERO_ENTRIES, False)
end_mat = time.perf_counter()
# Add convection term
start_lhs = time.perf_counter()
dolfinx.fem.petsc.assemble_matrix(A, convection_form)
A.assemble()
A.scale(-0.5)
A.axpy(1.0 / dt, M, PETSc.Mat.Structure.SUBSET_NONZERO_PATTERN)
A.axpy(-0.5 * nu, K, PETSc.Mat.Structure.SUBSET_NONZERO_PATTERN)
end_lhs = time.perf_counter()
# Do mat-vec operations
b.x.array[:] = 0
start_rhs = time.perf_counter()
A.mult(u_1.x.petsc_vec, b.x.petsc_vec)
b.x.scatter_reverse(dolfinx.la.InsertMode.add)
dolfinx.fem.petsc.set_bc(b.x.petsc_vec, bcs)
b.x.scatter_forward()
end_rhs = time.perf_counter()
t_matvec = end_rhs - start_rhs
mesh.comm.Barrier()
# Rescale matrix and apply bc
start_rescale = time.perf_counter()
A.scale(-1)
A.axpy(2 / dt, M, PETSc.Mat.Structure.SUBSET_NONZERO_PATTERN)
for bc in bcs:
A.zeroRowsLocal(bc._cpp_object.dof_indices()[0], 1.0) # type: ignore
end_rescale = time.perf_counter()
t_matrix = end_rescale - start_rescale + end_lhs - start_lhs
mesh.comm.Barrier()
# Gather results
oasis_lhs[i, :] = mesh.comm.allgather(t_matrix)
oasis_rhs[i, :] = mesh.comm.allgather(t_matvec)
oasis_total[i, :] = mesh.comm.allgather(t_matrix + t_matvec)
# ---------------------------------------------------------
# Zero out time-dependent matrix
Ax.zeroEntries()
Ax.setOption(PETSc.Mat.Option.KEEP_NONZERO_PATTERN, True)
Ax.setOption(PETSc.Mat.Option.IGNORE_ZERO_ENTRIES, False)
mesh.comm.Barrier()
# Add convection term
start_lhs_new = time.perf_counter()
dolfinx.fem.petsc.assemble_matrix(Ax, convection_form)
Ax.assemble()
Ax.scale(0.5)
Ax.axpy(1.0 / dt, M, PETSc.Mat.Structure.SUBSET_NONZERO_PATTERN)
Ax.axpy(0.5 * nu, K, PETSc.Mat.Structure.SUBSET_NONZERO_PATTERN)
for bc in bcs:
Ax.zeroRowsLocal(bc._cpp_object.dof_indices()[0], 1.0) # type: ignore
end_lhs_new = time.perf_counter()
mesh.comm.Barrier()
# Compute the vector without using pre-generated matrices
bx.x.array[:] = 0
start_rhs_new = time.perf_counter()
dolfinx.fem.petsc.assemble_vector(bx.x.petsc_vec, rhs_form)
bx.x.scatter_reverse(dolfinx.la.InsertMode.add)
dolfinx.fem.petsc.set_bc(bx.x.petsc_vec, bcs)
bx.x.scatter_forward()
end_rhs_new = time.perf_counter()
# Gather results
new_total[i, :] = mesh.comm.allgather(
end_lhs_new - start_lhs_new + end_rhs_new - start_rhs_new
)
new_lhs[i, :] = mesh.comm.allgather(end_lhs_new - start_lhs_new)
new_rhs[i, :] = mesh.comm.allgather(end_rhs_new - start_rhs_new)
matrix_total = mesh.comm.allgather(end_mat - start_mat)
if mesh.comm.rank == 0:
print(
"Oasis Total",
oasis_total[i],
"\nNew Total",
new_total[i],
"\nMatrix total",
matrix_total,
flush=True,
)
# Check that vectors are the same
if not np.allclose(bx.x.array, b.x.array):
print(np.max(np.abs(bx.x.array[:] - b.x.array[:])))
raise RuntimeError("Vectors are not equal after assembly")
# Check that matrices are the same
D.zeroEntries()
A.copy(D, PETSc.Mat.Structure.DIFFERENT_NONZERO_PATTERN)
D.axpy(-1, Ax, PETSc.Mat.Structure.DIFFERENT_NONZERO_PATTERN)
if not np.allclose(D.getValuesCSR()[2], 0):
print(np.max(np.abs(D.getValuesCSR()[2])))
raise RuntimeError("Matrices are not equal after assembly")
num_dofs_global = V.dofmap.index_map_bs * V.dofmap.index_map.size_global
return num_dofs_global, new_lhs, new_rhs, oasis_lhs, oasis_rhs, oasis_total, new_total
We solve the problem on a unit cube that is split into tetrahedra with Nx,Ny and Nx
tetrahedra in the x, y and z-direction respectively.
def run_parameter_sweep(
Nx: int, Ny: int, Nz: int, repeats: int, min_degree: int, max_degree: int
) -> dict:
# Information regarding optimization flags can be found at:
# https://gcc.gnu.org/onlinedocs/gcc/Optimize-Options.html
jit_options = {"cffi_extra_compile_args": ["-march=native", "-O3"]}
mesh = dolfinx.mesh.create_unit_cube(MPI.COMM_WORLD, Nx, Ny, Nz)
Ps = np.arange(min_degree, max_degree + 1, dtype=np.int32)
j = 0
results = {}
for i, P in enumerate(Ps):
if mesh.comm.rank == 0:
print(i, P, flush=True)
dof, new_lhs, new_rhs, oasis_lhs, oasis_rhs, oasis_total, new_total = assembly(
mesh, P, repeats=repeats, jit_options=jit_options
)
if mesh.comm.rank == 0:
print("Writing to dict")
for row in new_lhs:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "new",
"side": "lhs",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
for row in new_rhs:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "new",
"side": "rhs",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
for row in oasis_lhs:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "oasis",
"side": "lhs",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
for row in oasis_rhs:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "oasis",
"side": "rhs",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
for row in oasis_total:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "oasis",
"side": "total",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
for row in new_total:
for process in row:
results[j] = {
"P": P,
"num_dofs": dof,
"method": "new",
"side": "total",
"time (s)": process,
"procs": MPI.COMM_WORLD.size,
}
j += 1
return results
We use pandas and seaborn to visualize the results
def create_plot(results: dict, outfile: str):
if MPI.COMM_WORLD.rank == 0:
df = pandas.DataFrame.from_dict(results, orient="index")
df["label"] = (
"P"
+ df["P"].astype(str)
+ " "
+ df["num_dofs"].astype(str)
+ " \n Comms: "
+ df["procs"].astype(str)
)
plt.figure()
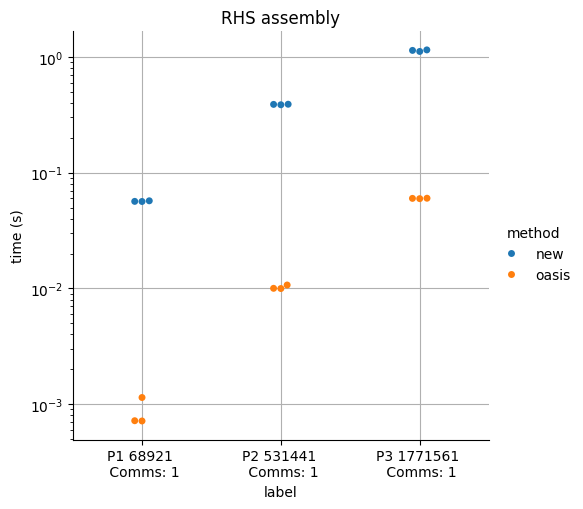
df_rhs = df[df["side"] == "rhs"]
plot = seaborn.catplot(data=df_rhs, kind="swarm", x="label", y="time (s)", hue="method")
plot.set(yscale="log", title="RHS assembly")
plt.grid()
plt.savefig(f"{outfile}_rhs.png")
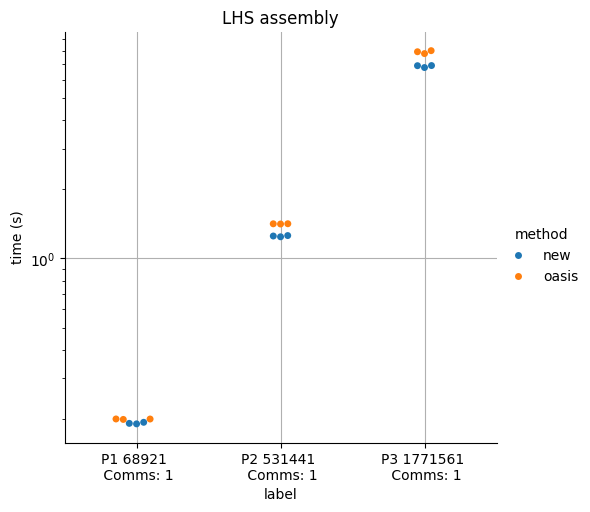
plt.figure()
df_lhs = df[df["side"] == "lhs"]
plot = seaborn.catplot(data=df_lhs, kind="swarm", x="label", y="time (s)", hue="method")
plot.set(yscale="log", title="LHS assembly")
plt.grid()
plt.savefig(f"{outfile}_lhs.png")
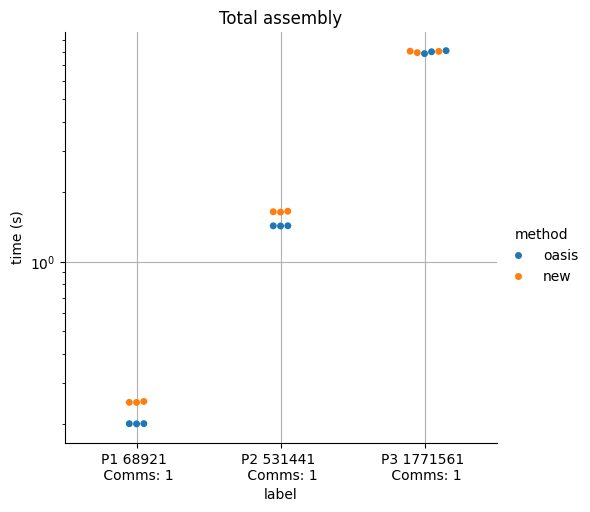
plt.figure()
df_total = df[df["side"] == "total"]
plot = seaborn.catplot(data=df_total, kind="swarm", x="label", y="time (s)", hue="method")
plot.set(yscale="log", title="Total assembly")
plt.grid()
plt.savefig(f"{outfile}_total.png")
# We start by running the comparison for an increasing number of degrees of freedom on a fixed grid.
if __name__ == "__main__":
N = 40
results_p = run_parameter_sweep(N, N, N, repeats=3, min_degree=1, max_degree=3)
create_plot(results_p, "results")
0 1
Oasis Total [0.19657611]
New Total [0.24691684]
Matrix total [0.00036016599995036813]
Oasis Total [0.19959825]
New Total [0.24841713]
Matrix total [0.00046489900000779016]
Oasis Total [0.19976612]
New Total [0.24828333]
Matrix total [0.0004893749999723696]
Writing to dict
1 2
Oasis Total [1.4266491]
New Total [1.63596342]
Matrix total [0.01301417899998114]
Oasis Total [1.43400498]
New Total [1.63503772]
Matrix total [0.0022759789999895474]
Oasis Total [1.43196093]
New Total [1.64770281]
Matrix total [0.0022615930000142725]
Writing to dict
2 3
Oasis Total [7.81926413]
New Total [7.808024]
Matrix total [0.07313428899999508]
Oasis Total [8.16095217]
New Total [8.10992853]
Matrix total [0.013621010999997907]
Oasis Total [8.24959714]
New Total [8.17017077]
Matrix total [0.012760106999962773]
Writing to dict
<Figure size 640x480 with 0 Axes>
<Figure size 640x480 with 0 Axes>
<Figure size 640x480 with 0 Axes>
