Regazzoni 2020 with a bleeding event#
In this example we will use the 0D model from [RSA+22] to simulate the cardiac cycle with a bleeding event. We use the Zenker model to find the heart rate for normal conditions and then we simulate a bleeding event and compute the new heart rate. Simularly we also adjust the systemic resistance and the contractility of the heart chambers to simulate the effects of bleeding.
from circulation.log import setup_logging
from circulation.regazzoni2020 import Regazzoni2020
from circulation.zenker import Zenker
import matplotlib.pyplot as plt
setup_logging()
# Run first Zenker to get the correct heart rate for normal conditions
zenker_normal = Zenker()
zenker_normal.solve(T=100.0, dt=1e-3, dt_eval=0.1)
history_zenker_normal = zenker_normal.history
HR_normal = history_zenker_normal["fHR"][-1]
R_TPR_normal = history_zenker_normal["R_TPR"][-1]
C_PRSW_normal = history_zenker_normal["C_PRSW"][-1]
[07/01/25 08:23:21] INFO INFO:circulation.base: base.py:132 Circulation model parameters (Zenker) ┏━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ kE_LV │ 0.066 / milliliter │ │ V_ED0 │ 7.14 milliliter │ │ P0_LV │ 2.03 millimeter_Hg │ │ tau_Baro │ 20.0 second │ │ k_width │ 0.1838 / millimeter_Hg │ │ Pa_set │ 70.0 millimeter_Hg │ │ Ca │ 4.0 milliliter / millimeter_Hg │ │ Cv │ 111.11 milliliter / millimeter_Hg │ │ Va0 │ 700 milliliter │ │ Vv0_min │ 2700 milliliter │ │ Vv0_max │ 3100 milliliter │ │ R_TPR_min │ 0.5335 millimeter_Hg * second / milliliter │ │ R_TPR_max │ 2.134 millimeter_Hg * second / milliliter │ │ T_sys │ 0.26666666666666666 second │ │ f_HR_min │ 0.6666666666666666 / second │ │ f_HR_max │ 3.0 / second │ │ R_valve │ 0.0025 millimeter_Hg * second / milliliter │ │ C_PRSW_min │ 25.9 millimeter_Hg │ │ C_PRSW_max │ 103.8 millimeter_Hg │ │ start_withdrawal │ 0.0 second │ │ end_withdrawal │ 0.0 second │ │ start_infusion │ 0.0 second │ │ end_infusion │ 0.0 second │ │ flow_withdrawal │ 0.0 milliliter / second │ │ flow_infusion │ 0.0 milliliter / second │ └──────────────────┴────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:138 Circulation model initial states (Zenker) ┏━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_ES │ 14.288 milliliter │ │ V_ED │ 21.432000000000002 milliliter │ │ S │ 0.5 dimensionless │ │ Va │ 938.1944444444443 milliliter │ │ Vv │ 3886.805555555555 milliliter │ └───────┴───────────────────────────────┘
print(f"HR_normal = {HR_normal}, R_TPR_normal = {R_TPR_normal}, C_PRSW_normal = {C_PRSW_normal}")
HR_normal = 1.839239834801396, R_TPR_normal = 1.3378014381141288, C_PRSW_normal = 65.04719277044089
# # Now we will simulate a bleeding and compute a new heart rate
blood_loss_parameters = {"start_withdrawal": 1, "end_withdrawal": 2, "flow_withdrawal": -2000, "flow_infusion": 0}
zenker_bleed = Zenker(parameters=blood_loss_parameters)
zenker_bleed.solve(T=300.0, dt=1e-3, dt_eval=0.1, initial_state=zenker_normal.state)
history_zenker_bleed = zenker_bleed.history
HR_bleed = history_zenker_bleed["fHR"][-1]
R_TPR_bleed = history_zenker_bleed["R_TPR"][-1]
C_PRSW_bleed = history_zenker_bleed["C_PRSW"][-1]
INFO INFO:circulation.base: base.py:132 Circulation model parameters (Zenker) ┏━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ kE_LV │ 0.066 / milliliter │ │ V_ED0 │ 7.14 milliliter │ │ P0_LV │ 2.03 millimeter_Hg │ │ tau_Baro │ 20.0 second │ │ k_width │ 0.1838 / millimeter_Hg │ │ Pa_set │ 70.0 millimeter_Hg │ │ Ca │ 4.0 milliliter / millimeter_Hg │ │ Cv │ 111.11 milliliter / millimeter_Hg │ │ Va0 │ 700 milliliter │ │ Vv0_min │ 2700 milliliter │ │ Vv0_max │ 3100 milliliter │ │ R_TPR_min │ 0.5335 millimeter_Hg * second / milliliter │ │ R_TPR_max │ 2.134 millimeter_Hg * second / milliliter │ │ T_sys │ 0.26666666666666666 second │ │ f_HR_min │ 0.6666666666666666 / second │ │ f_HR_max │ 3.0 / second │ │ R_valve │ 0.0025 millimeter_Hg * second / milliliter │ │ C_PRSW_min │ 25.9 millimeter_Hg │ │ C_PRSW_max │ 103.8 millimeter_Hg │ │ start_withdrawal │ 1 │ │ end_withdrawal │ 2 │ │ start_infusion │ 0.0 second │ │ end_infusion │ 0.0 second │ │ flow_withdrawal │ -2000 │ │ flow_infusion │ 0 │ └──────────────────┴────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:138 Circulation model initial states (Zenker) ┏━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_ES │ 14.288 milliliter │ │ V_ED │ 21.432000000000002 milliliter │ │ S │ 0.5 dimensionless │ │ Va │ 938.1944444444443 milliliter │ │ Vv │ 3886.805555555555 milliliter │ └───────┴───────────────────────────────┘
print(f"HR_bleed = {HR_bleed}, R_TPR_bleed = {R_TPR_bleed}, C_PRSW_bleed = {C_PRSW_bleed}")
HR_bleed = 2.999997254656593, R_TPR_bleed = 2.1339981168905187, C_PRSW_bleed = 103.79990834474941
HR_factor = HR_bleed / HR_normal
R_TPR_factor = R_TPR_bleed / R_TPR_normal
C_PRSW_factor = C_PRSW_bleed / C_PRSW_normal
regazzoni_normal_parmeters = Regazzoni2020.default_parameters()
regazzoni_normal_parmeters["HR"] = 1.0
regazzoni_normal = Regazzoni2020(parameters=regazzoni_normal_parmeters)
regazzoni_normal.print_info()
INFO INFO:circulation.base: base.py:132 Circulation model parameters (Regazzoni2020) ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ HR │ 1.0 │ │ chambers.LA.EA │ 0.07 millimeter_Hg / milliliter │ │ chambers.LA.EB │ 0.09 millimeter_Hg / milliliter │ │ chambers.LA.TC │ 0.17 second │ │ chambers.LA.TR │ 0.17 second │ │ chambers.LA.tC │ 0.8 second │ │ chambers.LA.V0 │ 4.0 milliliter │ │ chambers.LV.EA │ 2.75 millimeter_Hg / milliliter │ │ chambers.LV.EB │ 0.08 millimeter_Hg / milliliter │ │ chambers.LV.TC │ 0.34 second │ │ chambers.LV.TR │ 0.17 second │ │ chambers.LV.tC │ 0.0 second │ │ chambers.LV.V0 │ 5.0 milliliter │ │ chambers.RA.EA │ 0.06 millimeter_Hg / milliliter │ │ chambers.RA.EB │ 0.07 millimeter_Hg / milliliter │ │ chambers.RA.TC │ 0.17 second │ │ chambers.RA.TR │ 0.17 second │ │ chambers.RA.tC │ 0.8 second │ │ chambers.RA.V0 │ 4.0 milliliter │ │ chambers.RV.EA │ 0.55 millimeter_Hg / milliliter │ │ chambers.RV.EB │ 0.05 millimeter_Hg / milliliter │ │ chambers.RV.TC │ 0.34 second │ │ chambers.RV.TR │ 0.17 second │ │ chambers.RV.tC │ 0.0 second │ │ chambers.RV.V0 │ 10.0 milliliter │ │ valves.MV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.MV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.AV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.AV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.TV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.TV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.PV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.PV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ circulation.SYS.R_AR │ 0.8 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_AR │ 1.2 milliliter / millimeter_Hg │ │ circulation.SYS.R_VEN │ 0.26 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_VEN │ 130.0 milliliter / millimeter_Hg │ │ circulation.SYS.L_AR │ 0.005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.SYS.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.R_AR │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_AR │ 10.0 milliliter / millimeter_Hg │ │ circulation.PUL.R_VEN │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_VEN │ 16.0 milliliter / millimeter_Hg │ │ circulation.PUL.L_AR │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.external.start_withdrawal │ 0.0 second │ │ circulation.external.end_withdrawal │ 0.0 second │ │ circulation.external.start_infusion │ 0.0 second │ │ circulation.external.end_infusion │ 0.0 second │ │ circulation.external.flow_withdrawal │ 0.0 milliliter / second │ │ circulation.external.flow_infusion │ 0.0 milliliter / second │ └───────────────────────────────────────┴─────────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:138 Circulation model initial states (Regazzoni2020) ┏━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_LA │ 65.0 milliliter │ │ V_LV │ 120.0 milliliter │ │ V_RA │ 65.0 milliliter │ │ V_RV │ 145.0 milliliter │ │ p_AR_SYS │ 80.0 millimeter_Hg │ │ p_VEN_SYS │ 30.0 millimeter_Hg │ │ p_AR_PUL │ 35.0 millimeter_Hg │ │ p_VEN_PUL │ 24.0 millimeter_Hg │ │ Q_AR_SYS │ 0.0 milliliter / second │ │ Q_VEN_SYS │ 0.0 milliliter / second │ │ Q_AR_PUL │ 0.0 milliliter / second │ │ Q_VEN_PUL │ 0.0 milliliter / second │ └───────────┴─────────────────────────┘
INFO INFO:circulation.base: base.py:423 Volumes ┏━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 65.000 │ 120.000 │ 65.000 │ 145.000 │ 96.000 │ 3900.000 │ 350.000 │ 384.000 │ 395.000 │ 3996.000 │ 734.000 │ 5125.000 │ └────────┴─────────┴────────┴─────────┴──────────┴───────────┴──────────┴───────────┴─────────┴──────────┴─────────┴──────────┘ Pressures ┏━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ 80.000 │ 30.000 │ 35.000 │ 24.000 │ └───────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ 0.000 │ └───────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘
dt_eval = 0.01
regazzoni_normal.solve(num_beats=20, dt_eval=dt_eval)
N_normal = int(regazzoni_normal.HR / dt_eval)
regazzoni_bleed_parmeters = Regazzoni2020.default_parameters()
regazzoni_bleed_parmeters["HR"] = HR_factor
regazzoni_bleed_parmeters["circulation"]["SYS"]["R_AR"] *= R_TPR_factor
regazzoni_bleed_parmeters["circulation"]["SYS"]["R_VEN"] *= R_TPR_factor
for chamber in ["LA", "LV", "RA", "RV"]:
regazzoni_bleed_parmeters["chambers"][chamber]["EA"] *= C_PRSW_factor
regazzoni_bleed_parmeters["chambers"][chamber]["EB"] *= C_PRSW_factor
regazzoni_bleed_parmeters["circulation"]["external"] = blood_loss_parameters
regazzoni_bleed = Regazzoni2020(parameters=regazzoni_bleed_parmeters)
regazzoni_bleed.solve(num_beats=100, initial_state=regazzoni_normal.state, dt_eval=dt_eval)
regazzoni_bleed.print_info()
N_bleed = int(regazzoni_bleed.HR / dt_eval)
history_regazzoni_normal = regazzoni_normal.history
history_regazzoni_bleed = regazzoni_bleed.history
INFO INFO:circulation.base: base.py:132 Circulation model parameters (Regazzoni2020) ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ HR │ 1.6311071551908496 │ │ chambers.LA.EA │ 0.11170341523845612 millimeter_Hg / milliliter │ │ chambers.LA.EB │ 0.14361867673515785 millimeter_Hg / milliliter │ │ chambers.LA.TC │ 0.17 second │ │ chambers.LA.TR │ 0.17 second │ │ chambers.LA.tC │ 0.8 second │ │ chambers.LA.V0 │ 4.0 milliliter │ │ chambers.LV.EA │ 4.38834845579649 millimeter_Hg / milliliter │ │ chambers.LV.EB │ 0.127661045986807 millimeter_Hg / milliliter │ │ chambers.LV.TC │ 0.34 second │ │ chambers.LV.TR │ 0.17 second │ │ chambers.LV.tC │ 0.0 second │ │ chambers.LV.V0 │ 5.0 milliliter │ │ chambers.RA.EA │ 0.09574578449010523 millimeter_Hg / milliliter │ │ chambers.RA.EB │ 0.11170341523845612 millimeter_Hg / milliliter │ │ chambers.RA.TC │ 0.17 second │ │ chambers.RA.TR │ 0.17 second │ │ chambers.RA.tC │ 0.8 second │ │ chambers.RA.V0 │ 4.0 milliliter │ │ chambers.RV.EA │ 0.877669691159298 millimeter_Hg / milliliter │ │ chambers.RV.EB │ 0.07978815374175437 millimeter_Hg / milliliter │ │ chambers.RV.TC │ 0.34 second │ │ chambers.RV.TR │ 0.17 second │ │ chambers.RV.tC │ 0.0 second │ │ chambers.RV.V0 │ 10.0 milliliter │ │ valves.MV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.MV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.AV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.AV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.TV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.TV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.PV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.PV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ circulation.SYS.R_AR │ 1.2761224834075657 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_AR │ 1.2 milliliter / millimeter_Hg │ │ circulation.SYS.R_VEN │ 0.41473980710745884 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_VEN │ 130.0 milliliter / millimeter_Hg │ │ circulation.SYS.L_AR │ 0.005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.SYS.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.R_AR │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_AR │ 10.0 milliliter / millimeter_Hg │ │ circulation.PUL.R_VEN │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_VEN │ 16.0 milliliter / millimeter_Hg │ │ circulation.PUL.L_AR │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.external.start_withdrawal │ 1 │ │ circulation.external.end_withdrawal │ 2 │ │ circulation.external.start_infusion │ 0.0 second │ │ circulation.external.end_infusion │ 0.0 second │ │ circulation.external.flow_withdrawal │ -2000 │ │ circulation.external.flow_infusion │ 0 │ └───────────────────────────────────────┴─────────────────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:138 Circulation model initial states (Regazzoni2020) ┏━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_LA │ 65.0 milliliter │ │ V_LV │ 120.0 milliliter │ │ V_RA │ 65.0 milliliter │ │ V_RV │ 145.0 milliliter │ │ p_AR_SYS │ 80.0 millimeter_Hg │ │ p_VEN_SYS │ 30.0 millimeter_Hg │ │ p_AR_PUL │ 35.0 millimeter_Hg │ │ p_VEN_PUL │ 24.0 millimeter_Hg │ │ Q_AR_SYS │ 0.0 milliliter / second │ │ Q_VEN_SYS │ 0.0 milliliter / second │ │ Q_AR_PUL │ 0.0 milliliter / second │ │ Q_VEN_PUL │ 0.0 milliliter / second │ └───────────┴─────────────────────────┘
INFO INFO:circulation.base: base.py:423 Volumes ┏━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 58.499 │ 63.036 │ 54.774 │ 75.735 │ 116.451 │ 4126.772 │ 293.917 │ 335.816 │ 252.044 │ 4243.223 │ 629.733 │ 5125.000 │ └────────┴────────┴────────┴────────┴──────────┴───────────┴──────────┴───────────┴─────────┴──────────┴─────────┴──────────┘ Pressures ┏━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 7.823 │ 7.402 │ 5.671 │ 5.240 │ 97.043 │ 31.744 │ 29.392 │ 20.989 │ └───────┴───────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 54.019 │ -0.001 │ 55.231 │ -0.000 │ 51.301 │ 62.868 │ 51.775 │ 81.099 │ └────────┴────────┴────────┴────────┴──────────┴───────────┴──────────┴───────────┘
V_LV_normal = history_regazzoni_normal["V_LV"][-N_normal:]
V_LV_ED = max(V_LV_normal)
V_LV_ES = min(V_LV_normal)
SV_normal = V_LV_ED - V_LV_ES
V_LV_bleed = history_regazzoni_bleed["V_LV"][-N_bleed:]
V_LV_ED = max(V_LV_bleed)
V_LV_ES = min(V_LV_bleed)
SV_bleed = V_LV_ED - V_LV_ES
print(f"SV_normal = {SV_normal}, SV_bleed = {SV_bleed}")
SV_normal = 87.8443531509827, SV_bleed = 34.0498454945654
fig, ax = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10, 5))
ax[0, 0].set_title("Normal")
ax[0, 0].plot(history_regazzoni_normal["V_LV"], history_regazzoni_normal["p_LV"], label="LV")
ax[0, 0].plot(history_regazzoni_normal["V_RV"], history_regazzoni_normal["p_RV"], label="RV")
ax[1, 0].plot(history_regazzoni_normal["V_LV"][-N_normal:], history_regazzoni_normal["p_LV"][-N_normal:], label="LV")
ax[1, 0].plot(history_regazzoni_normal["V_RV"][-N_normal:], history_regazzoni_normal["p_RV"][-N_normal:], label="RV")
ax[0, 1].set_title("Bleeding")
ax[0, 1].plot(history_regazzoni_bleed["V_LV"], history_regazzoni_bleed["p_LV"], label="LV")
ax[0, 1].plot(history_regazzoni_bleed["V_RV"], history_regazzoni_bleed["p_RV"], label="RV")
ax[1, 1].plot(history_regazzoni_bleed["V_LV"][-N_bleed:], history_regazzoni_bleed["p_LV"][-N_bleed:], label="LV")
ax[1, 1].plot(history_regazzoni_bleed["V_RV"][-N_bleed:], history_regazzoni_bleed["p_RV"][-N_bleed:], label="RV")
[<matplotlib.lines.Line2D at 0x7f1577ac6de0>]
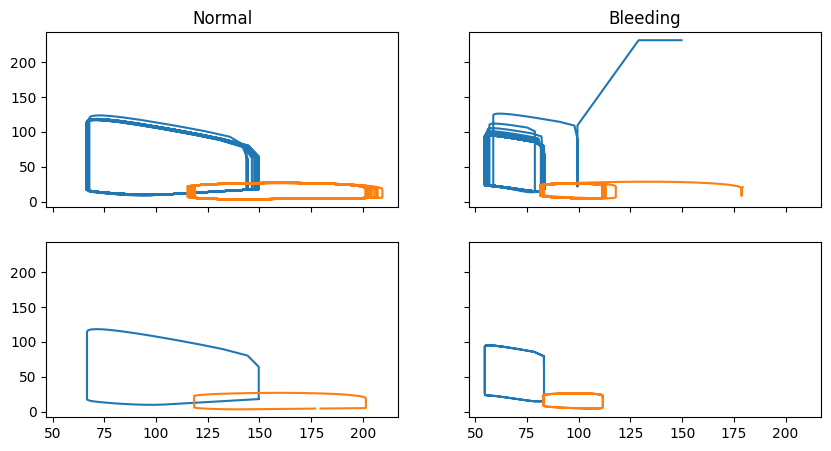
ax[0, 0].set_ylabel("p [mmHg]")
ax[1, 0].set_ylabel("p [mmHg]")
ax[1, 0].set_xlabel("V [mL]")
ax[1, 1].set_xlabel("V [mL]")
Text(0.5, 4.444444444444445, 'V [mL]')
for axi in ax.flatten():
axi.grid()
axi.legend()
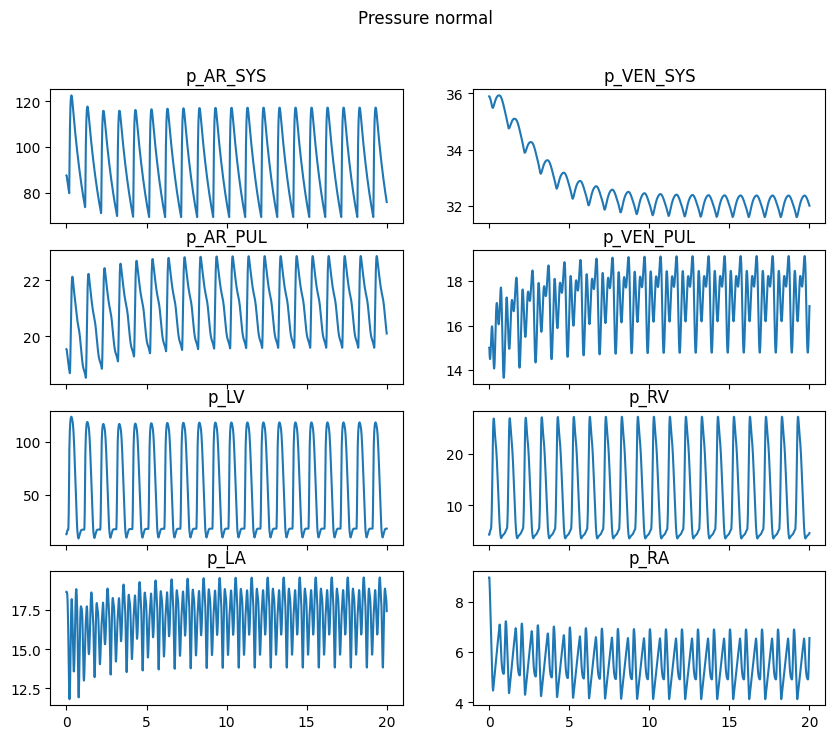
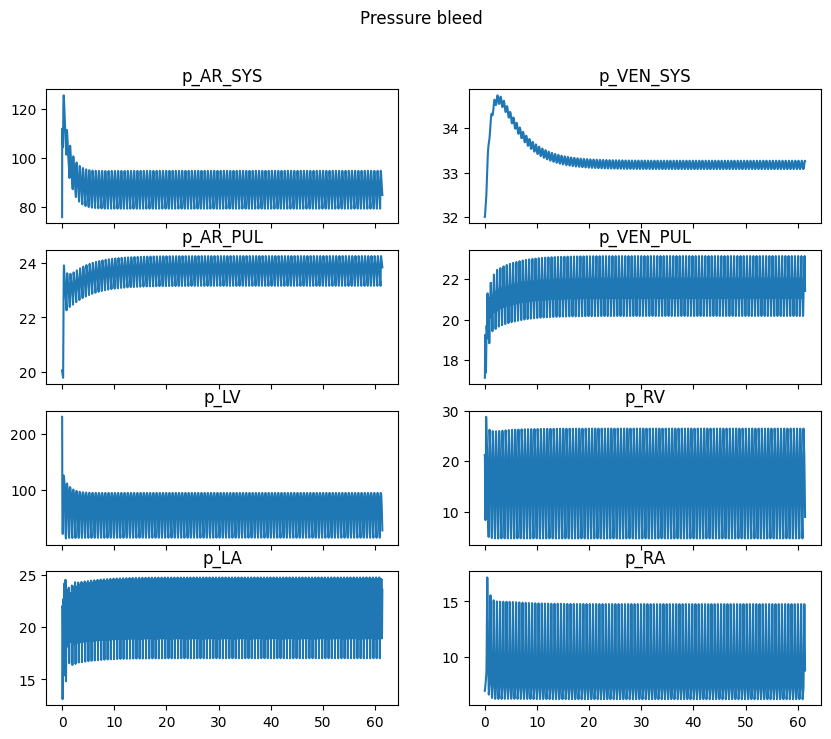
pressure_keys = ['p_AR_SYS', 'p_VEN_SYS', 'p_AR_PUL', 'p_VEN_PUL', 'p_LV', 'p_RV', 'p_LA', 'p_RA']
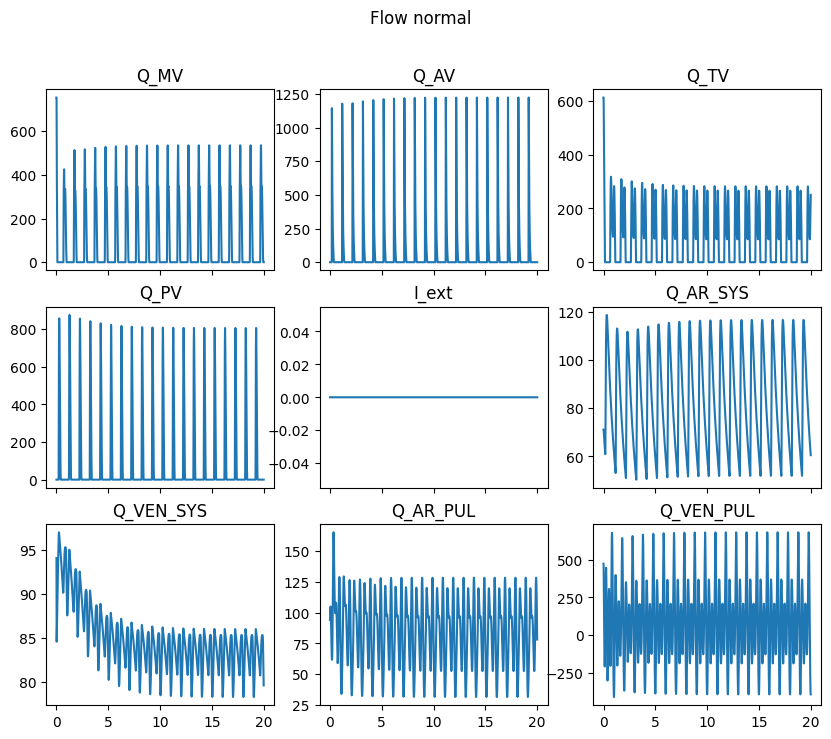
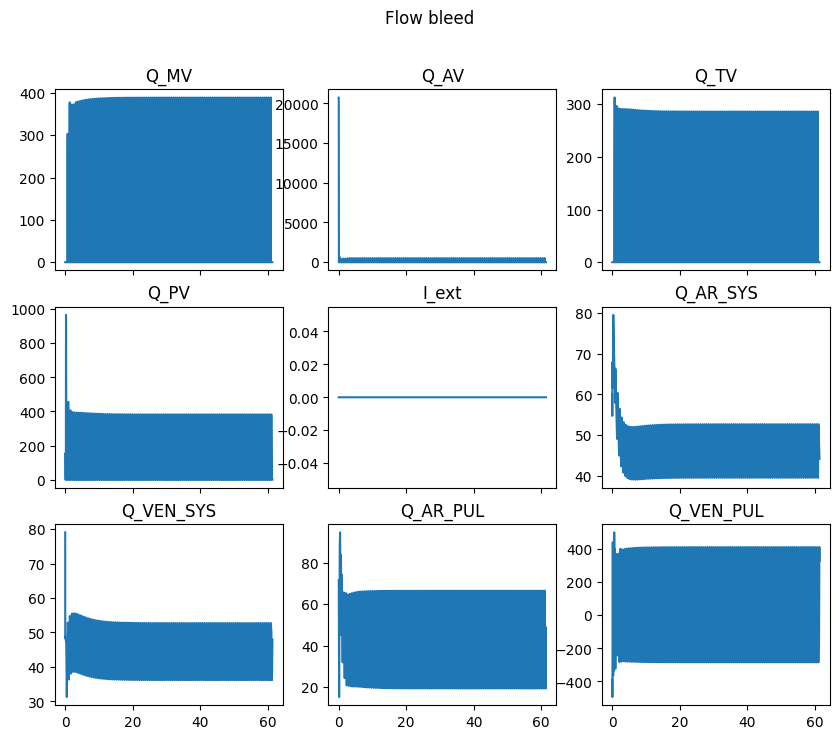
flow_keys = ["Q_MV","Q_AV", "Q_TV", "Q_PV" ,"I_ext", "Q_AR_SYS", "Q_VEN_SYS" , "Q_AR_PUL", "Q_VEN_PUL"]
for case, obj in [("normal",regazzoni_normal), ("bleed", regazzoni_bleed)]:
history = obj.history
fig, ax = plt.subplots(3, 3, sharex=True, figsize=(10, 8))
for axi, key in zip(ax.flatten(), flow_keys):
axi.plot(history["time"], history[key])
axi.set_title(key)
fig.suptitle(f"Flow {case}")
fig, ax = plt.subplots(4, 2, sharex=True, figsize=(10, 8))
for axi, key in zip(ax.flatten(), pressure_keys):
axi.plot(history["time"], history[key])
axi.set_title(key)
fig.suptitle(f"Pressure {case}")
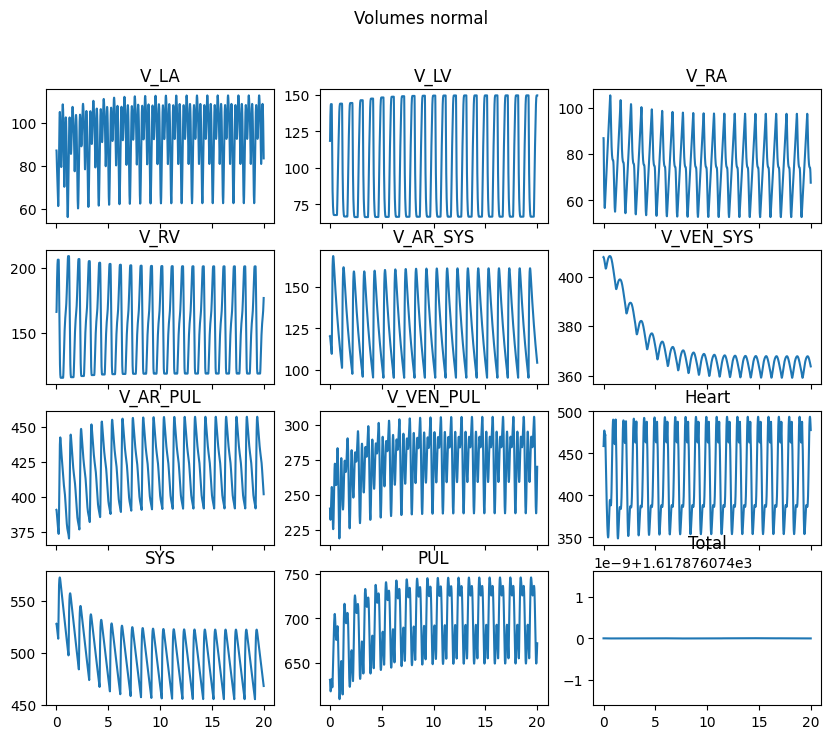
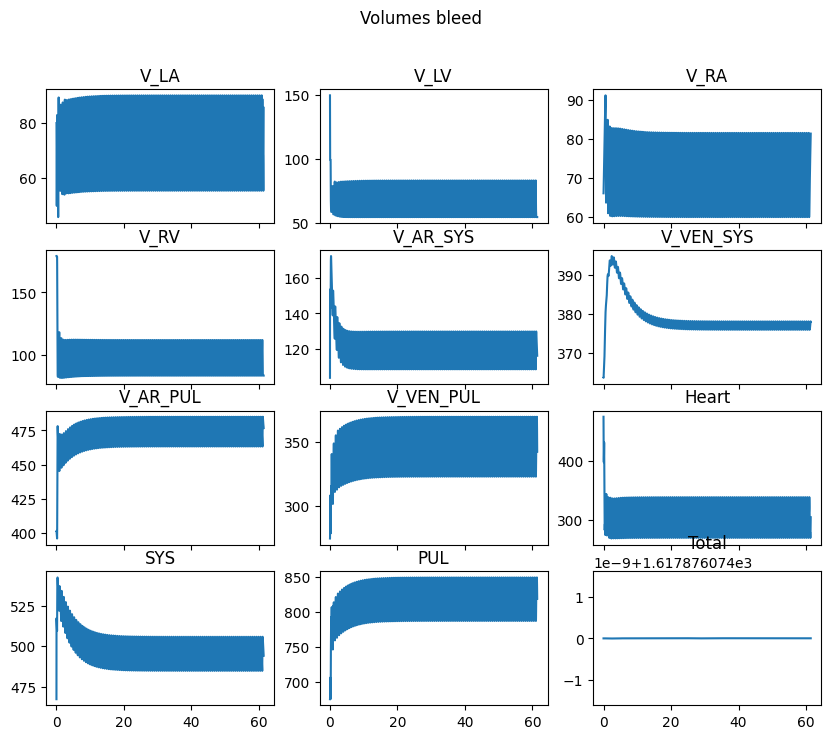
volumes = Regazzoni2020.compute_volumes(obj.parameters, obj.results_state)
fig, ax = plt.subplots(4, 3, sharex=True, figsize=(10, 8))
for axi, (key, v) in zip(ax.flatten(), volumes.items()):
axi.plot(history["time"], v)
axi.set_title(key)
fig.suptitle(f"Volumes {case}")
plt.show()
References#
[RSA+22]
Francesco Regazzoni, Matteo Salvador, Pasquale Claudio Africa, Marco Fedele, Luca Dedè, and Alfio Quarteroni. A cardiac electromechanical model coupled with a lumped-parameter model for closed-loop blood circulation. Journal of Computational Physics, 457:111083, 2022.