Regazzoni 2020#
In this example we will use the 0D model from [RSA+22] to simulate the cardiac cycle.
from circulation.log import setup_logging
from circulation.regazzoni2020 import Regazzoni2020
import matplotlib.pyplot as plt
setup_logging()
circulation = Regazzoni2020()
[07/01/25 08:23:15] INFO INFO:circulation.base: base.py:132 Circulation model parameters (Regazzoni2020) ┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ Parameter ┃ Value ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ HR │ 1.0 hertz │ │ chambers.LA.EA │ 0.07 millimeter_Hg / milliliter │ │ chambers.LA.EB │ 0.09 millimeter_Hg / milliliter │ │ chambers.LA.TC │ 0.17 second │ │ chambers.LA.TR │ 0.17 second │ │ chambers.LA.tC │ 0.8 second │ │ chambers.LA.V0 │ 4.0 milliliter │ │ chambers.LV.EA │ 2.75 millimeter_Hg / milliliter │ │ chambers.LV.EB │ 0.08 millimeter_Hg / milliliter │ │ chambers.LV.TC │ 0.34 second │ │ chambers.LV.TR │ 0.17 second │ │ chambers.LV.tC │ 0.0 second │ │ chambers.LV.V0 │ 5.0 milliliter │ │ chambers.RA.EA │ 0.06 millimeter_Hg / milliliter │ │ chambers.RA.EB │ 0.07 millimeter_Hg / milliliter │ │ chambers.RA.TC │ 0.17 second │ │ chambers.RA.TR │ 0.17 second │ │ chambers.RA.tC │ 0.8 second │ │ chambers.RA.V0 │ 4.0 milliliter │ │ chambers.RV.EA │ 0.55 millimeter_Hg / milliliter │ │ chambers.RV.EB │ 0.05 millimeter_Hg / milliliter │ │ chambers.RV.TC │ 0.34 second │ │ chambers.RV.TR │ 0.17 second │ │ chambers.RV.tC │ 0.0 second │ │ chambers.RV.V0 │ 10.0 milliliter │ │ valves.MV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.MV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.AV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.AV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.TV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.TV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ valves.PV.Rmin │ 0.0075 millimeter_Hg * second / milliliter │ │ valves.PV.Rmax │ 75006.2 millimeter_Hg * second / milliliter │ │ circulation.SYS.R_AR │ 0.8 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_AR │ 1.2 milliliter / millimeter_Hg │ │ circulation.SYS.R_VEN │ 0.26 millimeter_Hg * second / milliliter │ │ circulation.SYS.C_VEN │ 130.0 milliliter / millimeter_Hg │ │ circulation.SYS.L_AR │ 0.005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.SYS.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.R_AR │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_AR │ 10.0 milliliter / millimeter_Hg │ │ circulation.PUL.R_VEN │ 0.1625 millimeter_Hg * second / milliliter │ │ circulation.PUL.C_VEN │ 16.0 milliliter / millimeter_Hg │ │ circulation.PUL.L_AR │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.PUL.L_VEN │ 0.0005 millimeter_Hg * second ** 2 / milliliter │ │ circulation.external.start_withdrawal │ 0.0 second │ │ circulation.external.end_withdrawal │ 0.0 second │ │ circulation.external.start_infusion │ 0.0 second │ │ circulation.external.end_infusion │ 0.0 second │ │ circulation.external.flow_withdrawal │ 0.0 milliliter / second │ │ circulation.external.flow_infusion │ 0.0 milliliter / second │ └───────────────────────────────────────┴─────────────────────────────────────────────────┘
INFO INFO:circulation.base: base.py:138 Circulation model initial states (Regazzoni2020) ┏━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━┓ ┃ State ┃ Value ┃ ┡━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━┩ │ V_LA │ 65.0 milliliter │ │ V_LV │ 120.0 milliliter │ │ V_RA │ 65.0 milliliter │ │ V_RV │ 145.0 milliliter │ │ p_AR_SYS │ 80.0 millimeter_Hg │ │ p_VEN_SYS │ 30.0 millimeter_Hg │ │ p_AR_PUL │ 35.0 millimeter_Hg │ │ p_VEN_PUL │ 24.0 millimeter_Hg │ │ Q_AR_SYS │ 0.0 milliliter / second │ │ Q_VEN_SYS │ 0.0 milliliter / second │ │ Q_AR_PUL │ 0.0 milliliter / second │ │ Q_VEN_PUL │ 0.0 milliliter / second │ └───────────┴─────────────────────────┘
from scipy.integrate import solve_ivp
import numpy as np
res = solve_ivp( circulation.rhs, [0, 5], circulation.state_arr, t_eval=np.linspace(0, 5, 1000), method=”RK45”, max_step=1e-3, ) plt.plot(res.y[0, :]) plt.plot(res.y[1, :]) plt.show() breakpoint()
circulation.print_info() history = circulation.results
history = circulation.solve(num_beats=10)
circulation.print_info()
[07/01/25 08:23:19] INFO INFO:circulation.base: base.py:423 Volumes ┏━━━━━━━━┳━━━━━━━━━┳━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━┳━━━━━━━━━━┓ ┃ V_LA ┃ V_LV ┃ V_RA ┃ V_RV ┃ V_AR_SYS ┃ V_VEN_SYS ┃ V_AR_PUL ┃ V_VEN_PUL ┃ Heart ┃ SYS ┃ PUL ┃ Total ┃ ┡━━━━━━━━╇━━━━━━━━━╇━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━╇━━━━━━━━━━┩ │ 74.087 │ 135.887 │ 71.246 │ 165.457 │ 92.272 │ 3869.306 │ 347.703 │ 369.042 │ 446.676 │ 3961.578 │ 716.746 │ 5125.000 │ └────────┴─────────┴────────┴─────────┴──────────┴───────────┴──────────┴───────────┴─────────┴──────────┴─────────┴──────────┘ Pressures ┏━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ p_LA ┃ p_LV ┃ p_RA ┃ p_RV ┃ p_AR_SYS ┃ p_VEN_SYS ┃ p_AR_PUL ┃ p_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 10.866 │ 10.467 │ 8.460 │ 7.768 │ 76.893 │ 29.764 │ 34.770 │ 23.065 │ └────────┴────────┴───────┴───────┴──────────┴───────────┴──────────┴───────────┘ Flows ┏━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓ ┃ Q_MV ┃ Q_AV ┃ Q_TV ┃ Q_PV ┃ Q_AR_SYS ┃ Q_VEN_SYS ┃ Q_AR_PUL ┃ Q_VEN_PUL ┃ ┡━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩ │ 51.125 │ -0.001 │ 90.093 │ -0.000 │ 59.299 │ 81.867 │ 72.166 │ 74.828 │ └────────┴────────┴────────┴────────┴──────────┴───────────┴──────────┴───────────┘
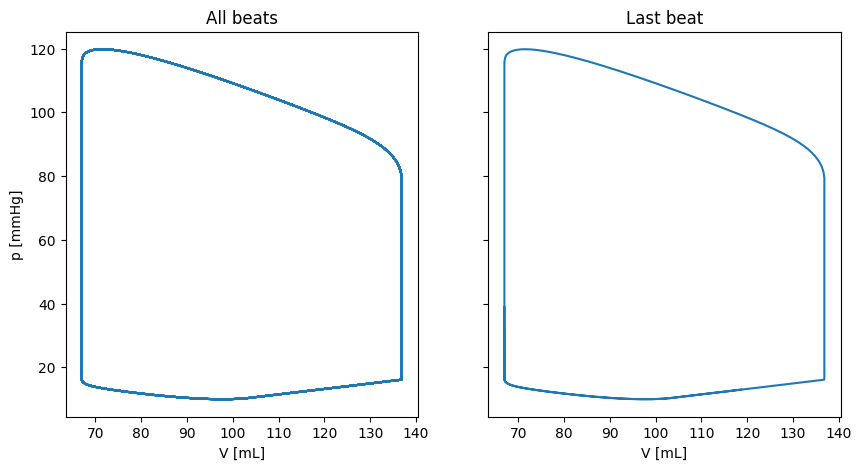
fig, ax = plt.subplots(1, 2, sharex=True, sharey=True, figsize=(10, 5))
ax[0].plot(history["V_LV"], history["p_LV"])
ax[0].set_xlabel("V [mL]")
ax[0].set_ylabel("p [mmHg]")
ax[0].set_title("All beats")
ax[1].plot(history["V_LV"][-1000:], history["p_LV"][-1000:])
ax[1].set_title("Last beat")
ax[1].set_xlabel("V [mL]")
Text(0.5, 0, 'V [mL]')
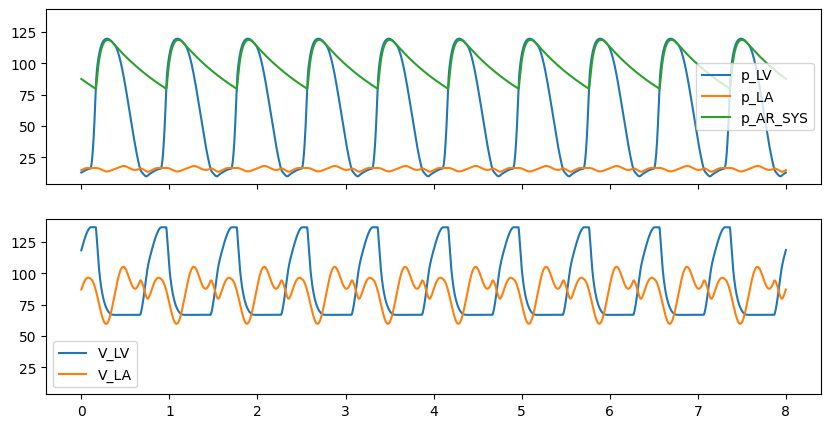
fig, ax = plt.subplots(2, 1, sharex=True, sharey=True, figsize=(10, 5))
ax[0].plot(history["time"], history["p_LV"], label="p_LV")
ax[0].plot(history["time"], history["p_LA"], label="p_LA")
ax[0].plot(history["time"], history["p_AR_SYS"], label="p_AR_SYS")
ax[0].legend()
ax[1].plot(history["time"], history["V_LV"], label="V_LV")
ax[1].plot(history["time"], history["V_LA"], label="V_LA")
ax[1].legend()
<matplotlib.legend.Legend at 0x7f3cb85e46b0>
plt.show()
References#
[RSA+22]
Francesco Regazzoni, Matteo Salvador, Pasquale Claudio Africa, Marco Fedele, Luca Dedè, and Alfio Quarteroni. A cardiac electromechanical model coupled with a lumped-parameter model for closed-loop blood circulation. Journal of Computational Physics, 457:111083, 2022.