Multi-cell model

In this demo we solve the Monodomain model using two different ionic models namely the ten-Tusscher model on the left side of the domain (\(x < 5.0\)) and the FitzHughNagumo model on the right side of the domain (\(x \geq 5\)). This can be useful if you want to model e.g fibrotic tissue, where parts of the tissue exhibit different properties than the rest of the tissue.

First we need to make the necessary imports

import math
import dolfin
import cbcbeat
import tqdm
from goss.dolfinutils import DOLFINParameterizedODE
from cbcbeat.gossplittingsolver import GOSSplittingSolver

Lets initializes some solver parameters

# Set-up solver
ps = GOSSplittingSolver.default_parameters()
ps["pde_solver"] = "monodomain"
ps["MonodomainSolver"]["linear_solver_type"] = "iterative"
ps["MonodomainSolver"]["theta"] = 0.5
ps["theta"] = 0.5
ps["enable_adjoint"] = False
ps["apply_stimulus_current_to_pde"] = True
ps["ode_solver"]["solver"] = "RL1"
ps["ode_solver"]["num_threads"] = 0
#

We define the domain, i.e a unit square that we scale by a factor of 10.0

domain = dolfin.UnitSquareMesh(100, 100)
domain.coordinates()[:] *= 10

Next we define the stimulus domain which will be a circle with

class StimSubDomain(dolfin.SubDomain):
    def __init__(self, center, radius):
        self.x0, self.y0 = center
        self.radius = radius
        super().__init__()

    def inside(self, x, on_boundary):
        r = math.sqrt((x[0] - self.x0) ** 2 + (x[1] - self.y0) ** 2)
        if r < self.radius:
            return True
        return False

# Create a mesh function containing markers for the stimulus domain
stim_domain = dolfin.MeshFunction("size_t", domain, domain.topology().dim(), 0)
# Set all markers to zero
stim_domain.set_all(0)
# We mark the stimulus domain with a different marker
stim_marker = 1
domain_size = domain.coordinates().max()
# Create a domain
stim_subdomain = StimSubDomain(
    center=(domain_size / 2.0, 0.0),
    radius=domain_size / 5.0,
)
# And mark the domain
stim_subdomain.mark(stim_domain, stim_marker)

Next we create the stimulus protocol

# Strength of the amplitude (this is based on the ionic model)
stim_amplitude = 50.0
# Duration of the stimulus
stim_duration = 1.0
# Make a constant representing time
time = dolfin.Constant(0.0)
# Make an expression that we apply a stimulus at 1 ms for a duration of 1 ms
stim = dolfin.Expression(
    "time > start ? (time <= (duration + start) ? " "amplitude : 0.0) : 0.0",
    time=time,
    duration=stim_duration,
    start=1.0,
    amplitude=stim_amplitude,
    degree=2,
)
# Make a stimulus object to be passed to cbcbeat
stimulus = cbcbeat.Markerwise([stim], [stim_marker], stim_domain)

Now, lets define the two ionic models. First we load the Tentussscher model

tentusscher = DOLFINParameterizedODE(
    "tentusscher_panfilov_2006_epi_cell.ode",
    field_states=["V"],
    field_parameters=["g_CaL"],
)
tentusscher_label = 10

Here we want to make sure the membrane potential is a field state. We also add a field parameter in order to make the conductance of the L-type calcium channel spatial dependent.

Next we load the the Fitzhugh-Nagumo model

fitzhughnagumo = DOLFINParameterizedODE(
    "fitzhughnagumo.ode",
    field_states=["V"],
    field_parameters=["b"],
)
fitzhughnagumo_label = 20

Similar as in the Tentusscher model we let the membrane potential be a field state. It is actually a requirement from goss that if we have multiple models inside of the domain, then they need to have the same field states. Also here we add a field parameter in order to make things a bit more interesting.

Lets also collect the models and the labels we will use for the different subdomains

cellmodels = [tentusscher, fitzhughnagumo]
labels = [tentusscher_label, fitzhughnagumo_label]

We also make sure that both domains have the same initial conditions for the membrane potential

for cellmodel in cellmodels:
    cellmodel.set_initial_conditions(V=-86.2)

Now we define the subdomains for the two different cell models

# Create subdomains for applying the different ODEs
subdomain = dolfin.CompiledSubDomain("x[0] <= 5.0")
cellmodel_domains = dolfin.MeshFunction("size_t", domain, 0)
# Set all markers to 10
cellmodel_domains.set_all(tentusscher_label)
# Set the marked domains to 20
subdomain.mark(cellmodel_domains, fitzhughnagumo_label)
cellmodels = cbcbeat.MultiCellModel(
    cellmodels,
    labels,
    cellmodel_domains,
)

Now let us set the field parameters. To do so, we first need to create an appropriate function space

# Create scalar FunctionSpace
V = dolfin.FunctionSpace(domain, "CG", 1)
L = domain.coordinates().max()

# Make an expression for a spatially varying parameter
param_scale = dolfin.Expression(
    "offset+scale*exp(-((x[0]-center_x)*(x[0]-center_x)+"
    "(x[1]-center_y)*(x[1]-center_y))/(sigma*sigma))",
    center_x=3 * L / 4,
    center_y=L / 4,
    offset=0.0,
    sigma=L / 2,
    scale=1.0,
    degree=2,
)

Set the field parameter in the tentusscher model

# Tentusscher parameter
ode_tt = cellmodels[tentusscher_label]
g_CaL_0 = ode_tt.get_parameter("g_CaL")
param_scale.offset = g_CaL_0
param_scale.scale = -g_CaL_0 * 0.95
param_scale.center_y = 3 * L / 4
g_CaL_func = dolfin.Function(V)
g_CaL_func.interpolate(param_scale)
ode_tt.set_parameter("g_CaL", g_CaL_func)

and the field parameter in the Fitzhugh-Nagumo model

ode_fhn = cellmodels[fitzhughnagumo_label]
k = 0.00004
V_rest = -85.0
V_threshold = -70.0
V_peak = 40.0
V_amp = V_peak - V_rest
l = 0.63  # noqa: E741
b = 0.013
param_scale.scale = b
param_scale.offset = b
param_scale.center_x = L / 4
param_scale.center_y = L / 4
b_func = dolfin.Function(V)
b_func.interpolate(param_scale)
cell_parameters = {
    "c_1": k * V_amp**2,
    "c_2": k * V_amp,
    "c_3": b / l,
    "a": (V_threshold - V_rest) / V_amp,
    "b": b_func,
    "V_rest": V_rest,
    "V_peak": V_peak,
}
# Set FHN specific parameters
for params in cell_parameters.items():
    ode_fhn.set_parameter(*params)
#

Next we need to define the conductivity tensor similar as in Monodomain model

chi = 12000.0  # cm^{-1}
s_il = 300.0 / chi  # mS
s_it = s_il / 2  # mS
s_el = 200.0 / chi  # mS
s_et = s_el / 1.2  # mS
sl = s_il * s_el / (s_il + s_el)
st = s_it * s_et / (s_it + s_et)
M_i = dolfin.as_tensor(((dolfin.Constant(sl), 0), (0, dolfin.Constant(st))))

Create and the CardiacModel in cbcbeat.

heart = cbcbeat.CardiacModel(
    domain=domain,
    time=time,
    M_i=M_i,
    M_e=None,
    cell_models=cellmodels,
    stimulus=stimulus,
)

# and initialize the solver
solver = GOSSplittingSolver(heart, ps)

We extract the membrane potential from the solution fields

(vs_, vs, vur) = solver.solution_fields()
V = vs.function_space()
v = dolfin.Function(V)

and solve the model for 100 ms with increments of 0.5. We also save the resulting membrane potential in and XDMF file that can be visualized in Paraview.

dt = 0.5
T = 100
vfile = dolfin.XDMFFile(dolfin.MPI.comm_world, "multicell.xdmf")
for (t0, t1), fields in tqdm.tqdm(solver.solve((0, T), dt), total=int(T / dt)):
    v.assign(vs_)
    vfile.write(v, t0)

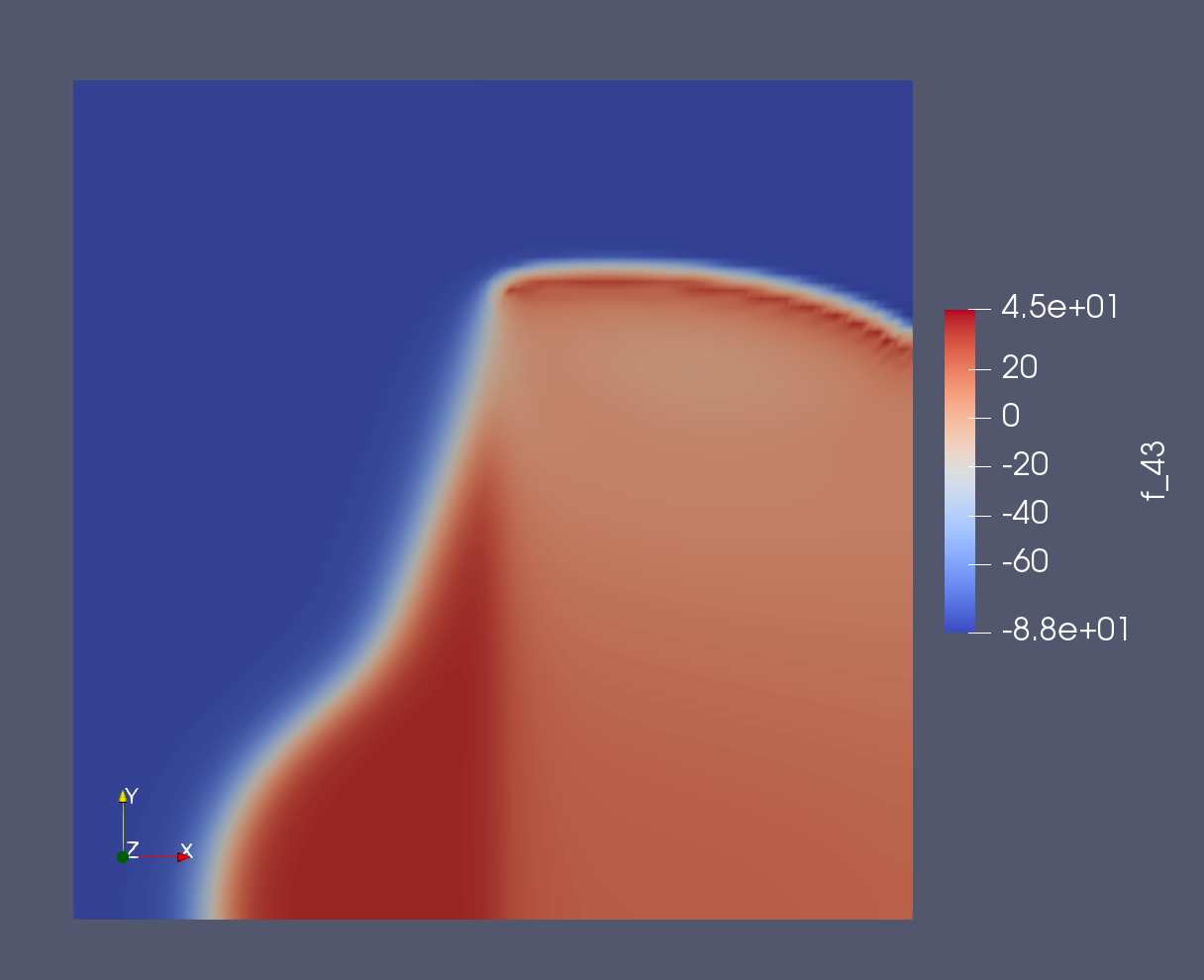
Fig. 10 Membrane potential

Reference