Custom model (pure EP)

In the current version of simcardems there are only three types of models, a strongly coupled model, an explicitly couple model and a pure EP model. All of these models use the same underlying cell model, and you might want to provide your own model.

In this demo we show you how to implement your own set of model. To make things a bit simpler we will implement a pure EP solver based on the Fitzhugh Nagumo model. For this demo we will copy the model from the cbcbeat library.

Note that if you want to only run pure EP simulations, then you could just use cbcbeat directly.

The model structure

Each model in the model in the models directory contains three different models; a cell model, an active model and a model for the EM coupling. When implementing a new model, you need to provide an implementation for all of these.

Implementing the EM coupling

We will start by implement the model for the EM coupling. First we will make the necessary imports.

import typing
import simcardems
import simcardems.save_load_functions as io
from pathlib import Path
from collections import OrderedDict
import dolfin
import cbcbeat
import matplotlib.pyplot as plt

try:
    import ufl_legacy as ufl
except ImportError:
    import ufl

simcardems provide an interface for this class which can be found in the em_model module. This class comes with some methods already implemented, but it is also possible to provide custom implementations of these methods. Note that all of the methods provided in this base class are used in some way when running a simulation

The full implementation of the class is shown below, where we have provided an implementation of the following methods

• register_ep_model - this is a method that takes in a cbcbeat.SplittingSolver and just sets this as an attribute on the instance.

• setup_assigners - this is a class for setting up which variables that you want to keep track of from the state. The state variable in the EP solver is a vector function containing all state variables (we will see that the Fitzhugh Nagumo model has two states; v and s). When running a simulation, you might want to store keep track of a subset of these state variables. In our case we want to keep track of the state variable at index 0 which we will name v. We also indicate that this belong to the ep group since we could also have state variables for the mechanics.

• solve_ep - this is the method that is called when you want to solve the EP. This takes in a tuple of two flows that indicate the time interval that you want to solve for.

• print_ep_info - this is a method that is called during that setup of the model and you can put any info here that you want to display about the EP model.

• cell_params - this should return a dictionary with the cell parameters from the cell model.

• ep_mesh - this is just a helper function for getting the mesh for the EP

• update_prev_ep - this is a method that is called after solving the EP model and will update the previous state solution.

• save_state - this is the method that is called when the simulation is done and the state is saved. In our case we would like to save the state from

• load_state - this method goes together with the save_state method and is used when you want to load an existing state from a file.

class EMCoupling(simcardems.models.em_model.BaseEMCoupling):
    def register_ep_model(self, solver: cbcbeat.SplittingSolver) -> None:
        self.ep_solver = solver

    def setup_assigners(self) -> None:
        from simcardems.datacollector import Assigners

        self._assigners = Assigners(vs=self.ep_solver.vs, mech_state=None)
        self.assigners.register_subfunction(
            name="v",
            group="ep",
            subspace_index=0,
        )

    def solve_ep(self, interval: typing.Tuple[float, float]) -> None:
        self.ep_solver.step(interval)

    def print_ep_info(self):
        # Output some degrees of freedom
        total_dofs = self.ep_solver.vs.function_space().dim()
        simcardems.utils.print_mesh_info(self.ep_mesh, total_dofs)

    def cell_params(self):
        return self.ep_solver.ode_solver._model.parameters()

    @property
    def ep_mesh(self):
        return self.geometry.ep_mesh

    def update_prev_ep(self):
        self.ep_solver.vs_.assign(self.ep_solver.vs)

    def save_state(
        self,
        path: typing.Union[str, Path],
        config: typing.Optional[simcardems.Config] = None,
    ) -> None:
        super().save_state(path=path, config=config)

        with dolfin.HDF5File(
            self.geometry.comm(),
            Path(path).as_posix(),
            "a",
        ) as h5file:
            h5file.write(self.ep_solver.vs, "/ep/vs")

        io.dict_to_h5(
            self.cell_params(),
            path,
            "ep/cell_params",
        )

    @classmethod
    def from_state(
        cls,
        path: typing.Union[str, Path],
        *args,
        **kwargs,
    ) -> simcardems.models.em_model.BaseEMCoupling:
        print(f"Load state from path {path}")
        path = Path(path)
        if not path.is_file():
            raise FileNotFoundError(f"File {path} does not exist")

        geo = simcardems.geometry.load_geometry(
            path,
            schema_path=path.with_suffix(".json"),
        )
        print("Open file with h5py")
        with io.h5pyfile(path) as h5file:
            config = simcardems.Config(**io.h5_to_dict(h5file["config"]))
            state_params = io.h5_to_dict(h5file["state_params"])
            cell_params = io.h5_to_dict(h5file["ep"]["cell_params"])
            vs_signature = h5file["ep"]["vs"].attrs["signature"].decode()

        VS = dolfin.FunctionSpace(geo.ep_mesh, eval(vs_signature))
        vs = dolfin.Function(VS)
        print("Load functions")
        with dolfin.HDF5File(geo.ep_mesh.mpi_comm(), path.as_posix(), "r") as h5file:
            h5file.read(vs, "/ep/vs")

        cell_inits = io.vs_functions_to_dict(
            vs,
            state_names=Fitzhughnagumo.default_initial_conditions().keys(),
        )

        return simcardems.models.em_model.setup_EM_model(
            cls_EMCoupling=cls,
            cls_CellModel=Fitzhughnagumo,
            cls_ActiveModel=None,
            geometry=geo,
            config=config,
            cell_inits=cell_inits,
            cell_params=cell_params,
            state_params=state_params,
        )

Implementing the Cell model

The cell model used in this demo is the Fitzhugh Nagumo model and the code is more or less copied from the cbcbeat library. The only major adjustment is that the cell model need to take in an additional argument coupling which is an instance of the EMCoupling class that we implemented above. In this case we are using this argument for anything, but in other cases you might want to pass additional function to the cell model, and you can do this using an instance of this EMCoupling class. You can check out the other models in the repository for examples of this.

class Fitzhughnagumo(cbcbeat.cellmodels.CardiacCellModel):
    def __init__(
        self,
        coupling: EMCoupling,
        params=None,
        init_conditions=None,
    ):
        """
        Create cardiac cell model

        *Arguments*
         params (dict, :py:class:`dolfin.Mesh`, optional)
           optional model parameters
         init_conditions (dict, :py:class:`dolfin.Mesh`, optional)
           optional initial conditions
        """
        print("Initialize Cell Model")
        super().__init__(params, init_conditions)

    @staticmethod
    def default_parameters(*args, **kwargs):
        "Set-up and return default parameters."
        params = OrderedDict(
            [
                ("a", 0.13),
                ("b", 0.013),
                ("c_1", 0.26),
                ("c_2", 0.1),
                ("c_3", 1.0),
                ("stim_amplitude", 0),
                ("stim_duration", 1),
                ("stim_period", 1000),
                ("stim_start", 1),
                ("v_peak", 40.0),
                ("v_rest", -85.0),
            ],
        )
        return params

    @staticmethod
    def default_initial_conditions():
        "Set-up and return default initial conditions."
        ic = OrderedDict([("v", -85.0), ("s", 0.0)])
        return ic

    def I(self, v, s, time=None):
        """
        Transmembrane current
        """
        # Imports
        # No imports for now

        time = time if time else dolfin.Constant(0.0)

        # Assign parameters
        a = self._parameters["a"]
        stim_start = self._parameters["stim_start"]
        stim_amplitude = self._parameters["stim_amplitude"]
        c_1 = self._parameters["c_1"]
        c_2 = self._parameters["c_2"]
        v_rest = self._parameters["v_rest"]
        stim_duration = self._parameters["stim_duration"]
        v_peak = self._parameters["v_peak"]

        current = (
            -(v - v_rest)
            * (v_peak - v)
            * (-(v_peak - v_rest) * a + v - v_rest)
            * c_1
            / ((v_peak - v_rest) * (v_peak - v_rest))
            + (v - v_rest) * c_2 * s / (v_peak - v_rest)
            - (1.0 - 1.0 / (1.0 + ufl.exp(-5.0 * stim_start + 5.0 * time)))
            * stim_amplitude
            / (1.0 + ufl.exp(-5.0 * stim_start + 5.0 * time - 5.0 * stim_duration))
        )

        return current

    def F(self, v, s, time=None):
        """
        Right hand side for ODE system
        """

        time = time if time else dolfin.Constant(0.0)

        # Assign parameters
        c_3 = self._parameters["c_3"]
        b = self._parameters["b"]
        v_rest = self._parameters["v_rest"]

        F_expressions = [
            # Derivative for state s
            (-c_3 * s + v - v_rest) * b,
        ]

        return F_expressions[0]

    def num_states(self):
        return 1

We are now ready to use the this new custom model. First, we need to load some geometry, and we will use the pre-made left ventricular geometry

geo = simcardems.geometry.load_geometry(mesh_path="geometries/lv_ellipsoid.h5")
# Next we create an instance of the `EMCoupling`. This is done by passing in the class for the `EMCoupling`, the `CellModel` and finally the `ActiveModel`. In our case, we don't want to include any mechanics, and therefore we set the `ActiveModel` to `None.
coupling = simcardems.models.em_model.setup_EM_model(
    cls_EMCoupling=EMCoupling,
    cls_CellModel=Fitzhughnagumo,
    cls_ActiveModel=None,
    geometry=geo,
)
# We also need to create the configuration, and we pass in the output directory and the `coupling_type`.
outdir = Path("result_custom_cell_model_pure_ep")
config = simcardems.Config(
    outdir=outdir,
    coupling_type=coupling.coupling_type,
)
# Now we create a runner for running the simulation
runner = simcardems.Runner.from_models(coupling=coupling, config=config)
# And then we run a simulation for 500 milliseconds
runner.solve(500)
# When the simulation is done we can load the results from the output directory using `simcardems.DataLoader`
loader = simcardems.DataLoader(outdir / "results.h5")
# We can extract the traces from the loader, and specify that the traces we want to extract should be the average over the mesh
values = simcardems.postprocess.extract_traces(loader, reduction="average")
# Now we can plt the state variable as a function of time
fig, ax = plt.subplots()
ax.plot(values["time"], values["ep"]["v"])
fig.savefig(outdir / "v.png")

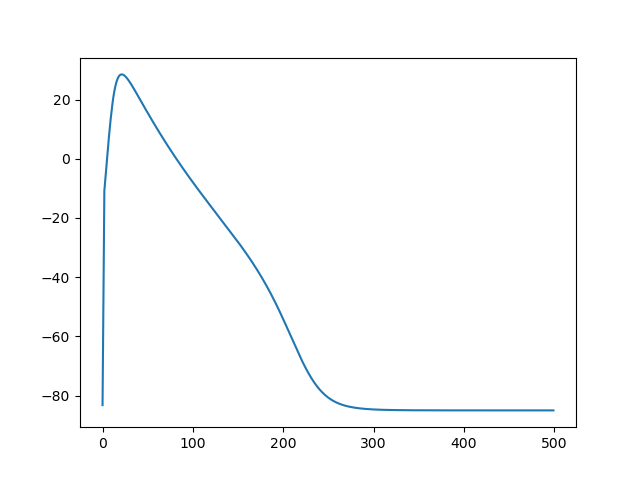
Fig. 7 Average value of the state variable \(v\)

# We can also create an `xdmf` file that we can visualize in Paraview
simcardems.postprocess.make_xdmffiles(outdir / "results.h5")

Movie showing \(v\) over time